冲击串的傅里叶变换

冲激信号的傅里叶变换

对于一个冲激信号，其傅里叶变换非常简单，就是“1”，冲击信号在频域中的地位就相当于在时域中的常数

单位冲激信号\delta(t) 的傅里叶变换：

\mathcal{F}\{\delta(t)\} = \int_{-\infty}^{\infty} \delta(t) e^{-j\omega t} dt

冲激函数具有筛选性质：

\int_{-\infty}^{\infty} \delta(t) f(t) dt = f(0)

所以冲击信号的傅里叶变换为：

\mathcal{F}\{\delta(t)\} = e^{-j\omega \cdot 0} = 1

冲击串的傅里叶变换推导

冲击串就是冲激信号在时域上周期延拓的效果，可以用来表示采样信号，表达式大概可以写成：\delta_T(t) = \sum_{n=-\infty}^{\infty} \delta(t - nT)，T是延拓的周期，图像上大概可以表示为：

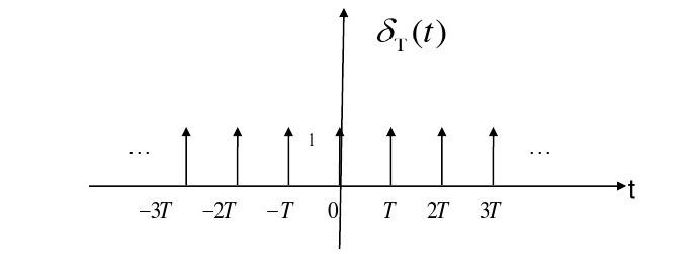
因为冲击串可以表示为一个周期函数，所以可以采用傅里叶级数展开表示：

\delta_T(t) = \sum_{k=-\infty}^{\infty}c_n e^{j k \omega_0 t}

其中：

c_n = \frac{1}{T} \int_{-T/2}^{T/2} \delta(t) e^{-j k \frac{2\pi n}{T} t} \, dt = \frac{1}{T}（还是筛选性质）

所以：

\delta_T(t) = \frac{1}{T} \sum_{k=-\infty}^{\infty} e^{j k \frac{2\pi n}{T} t}

这个式子表示在频域上，就是一连串的孤立的频域上的点，你可以通过傅里叶变换表达一下e^{j k \frac{2\pi n}{T} t}，他就是冲激再时移了\frac{n}{T},所以冲激函数串的频域表示还是冲激函数串，周期为\frac{1}{T}我们记S(\omega) 为冲激函数的频谱：

S(\omega) = \frac{1}{T}\sum^{\infty}_{n=-\infty}\delta(\omega-\frac{n}{T})

因此我们得出一个重要的结论，冲击串的频谱还是一个冲击串，周期为\frac{1}{T}

取样

当我们采用离散信号对连续信号取样时，可以等价为将原函数乘以冲击串得到的结果为我们的离散采样信号，也就是说

对采样后的信号做傅里叶变换可以得到：

将前面推导出来的冲击串的傅里叶变换带进去，框框一顿推导，我就不写了，这个公式编辑器太难用了，写出来以后结果像这样：

F_{采样} = \frac{1}{T}\sum_{n=-\infty}^{\infty}F(\omega-\frac{n}{T})

可以看出一个重要的性质！采样信号的频谱是原信号频谱的周期延拓！周期为\frac{1}{T}也就是采样率，他必须足够高，才能在各个副本之间有明显的区分

【明天写完...】